Хипократ на Хиос (ет. 460 г. пр. Н. Е.) Демонстрира, че облаците с форма на луна между кръговите дъги, известни като луни, могат да бъдат изразени точно като праволинейна област или квадратура. В следващия прост случай две луни, развити около страните на десен триъгълник, имат комбинирана площ, равна на тази на триъгълника.
-
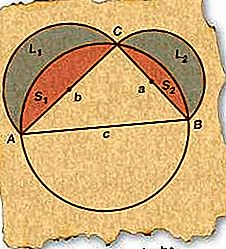
Започвайки отдясно ΔABC, нарисувайте кръг, чийто диаметър съвпада с AB (страна c), хипотенузата. Тъй като всеки десен триъгълник, начертан с диаметър на окръжност за неговата хипотенуза, трябва да бъде вписан в кръга, C трябва да е върху окръжността.
-
Начертайте полукръгове с диаметри AC (страна b) и BC (страна a), както е на фигурата.
-
Етикет получената Lunes L 1 и L 2 и получените сегменти S 1 и S 2, както е показано на фигурата.
-
Сега сумата на луните (L 1 и L 2) трябва да е равна на сумата на полукръговете (L 1 + S 1 и L 2 + S 2), съдържащи ги минус двата сегмента (S 1 и S 2). По този начин L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (тъй като площта на окръжност е π пъти по-голяма от квадрата на радиуса).
-
Сумата от сегментите (S 1 и S 2) е равна на площта на полукръга въз основа на AB минус площта на триъгълника. По този начин, S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Подмяна на израза от стъпка 5 в етап 4 и разделяне на общи термини, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Тъй като ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, по теоремата на Питагор. Така, L 1 + L 2 = ΔABC.
Хипократ успял да наклони няколко вида луни, някои от дъги по-големи и по-малки от полукръгове и той намекнал, макар че може би не е вярвал, че методът му може да квадратира цял кръг. В края на класическата епоха Боеций (ок. 470–524 г.), чиито латински преводи на фрагменти на Евклид ще запазят светлината на геометрията, трептяща в продължение на половин хилядолетие, спомена, че някой е извършил преграждането на кръга. Дали неизвестният гений е използвал луни или някакъв друг метод, не се знае, тъй като поради липса на място Боеций не даде демонстрация. По този начин той предаде предизвикателството на квадратурата на кръга заедно с фрагменти от геометрията, очевидно полезни при изпълнението му. Европейците се държаха на неудачната задача добре в Просвещението. И накрая, през 1775 г. Парижката академия на науките, изморена от задачата да забележи заблудите в многото решения, представени на нея, отказва да има нещо по-нататък с кръговите квадратчета.













