Математика на тензорния анализ

Тензорен анализ, клон на математиката, засягащ отношенията или законите, които остават валидни независимо от системата от координати, използвани за определяне на количествата. Такива отношения се наричат ​​ковариантни. Тензорите са измислени като разширение на векторите, за да се формализира манипулацията на геометрични образувания, възникващи при изучаването на математически многообразия.

Вектор е образувание, което има както величина, така и посока; той е представим чрез чертеж на стрела и се комбинира с подобни образувания съгласно паралелограмовия закон. Поради този закон, вектор има компоненти - различен набор за всяка координатна система. Когато координатната система е променена, компонентите на вектора се променят според математически закон на преобразуване, изводим от закона на паралелограма. Този закон на трансформация на компонентите има две важни свойства. Първо, след поредица от промени, които завършват в оригиналната координатна система, компонентите на вектора ще бъдат същите като в началото. Второ, връзките между векторите - например три вектора U, V, W, така че 2U + 5V = 4W - ще присъстват в компонентите, независимо от координатната система.

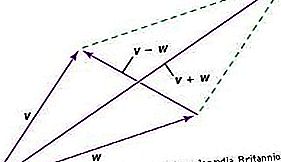
Следователно вектор може да се разглежда като образувание, което в n-измерното пространство има n компоненти, които се преобразуват съгласно специфичен закон на трансформация, притежаващ горните свойства. Самият вектор е обективна единица, независима от координатите, но се третира по отношение на компоненти с всички координатни системи на равна основа.

Без да настоява за изобразително изображение, тензорът се дефинира като обективна единица, която има компоненти, които се променят според закона за преобразуване, който е обобщение на закона за векторна трансформация, но който запазва двете ключови свойства на този закон. За удобство, координатите обикновено са номерирани от 1 до n, а всеки компонент на тензор се обозначава с буква, съдържаща суперскрипти и абонаменти, всяка от които независимо приема стойностите от 1 до n. По този начин, един тензор, представен от компонентите T ^ab _c, би имал n ³ компонента, като стойностите на a, b и c протичат от 1 до n. Скаларите и векторите представляват специални случаи на тензори, като първият притежава само един компонент на координатна система, а вторият притежава n. Всяко линейно отношение между тензорни компоненти, като7R ^a _bcd + 2S ^a _bcd - 3T ^a _bcd = 0, ако е валидно в една координатна система, е валидно за всички и по този начин представлява отношение, което е обективно и независимо от координатните системи, независимо от липса на изобразително представяне.

От особен интерес представляват два тензора, наречени метричен тензор и тензор на кривината. Метричният тензор се използва например за преобразуване на векторни компоненти във величини на векторите. За простота помислете за двумерния случай с прости перпендикулярни координати. Нека вектор V има компоненти V ₁, V ₂. Тогава чрез теоремата на Питагор, приложена към десния триъгълник OAP, квадратът с величината на V се дава byOP ² = (V ₁) ² + (V ₂) ².

Скрито в това уравнение е метричният тензор. Той е скрит, защото тук се състои от 0 и 1, които не са записани. Ако уравнението е пренаписано във форматаOP ² = 1 (V ₁) ² + 0V ₁ V ₂ + 0V ₂ V ₁ + 1 (V ₂) ², пълният набор от компоненти (1, 0, 0, 1) на метричния тензор е очевиден. Ако се използват наклонени координати, формулата за OP ² приема по-общата формаOP ² = g ₁₁ (V ₁) ² + g ₁₂ V ₁ V ₂ + g ₂₁ V ₂ V ₁ + g ₂₂ (V ₂) ², количествата g ₁₁, g ₁₂, g ₂₁, g ₂₂ са новите компоненти на метричния тензор.

Извън метричния тензор е възможно да се изгради сложен тензор, наречен тензор на кривината, който представлява различните аспекти на вътрешната кривина на n-мерното пространство, към което принадлежи.

Тенорите имат много приложения в геометрията и физиката. Създавайки своята обща теория на относителността, Алберт Айнщайн твърди, че законите на физиката трябва да бъдат еднакви, без значение каква координатна система се използва. Това го накара да изрази тези закони по отношение на тензорни уравнения. От неговата специална теория на относителността беше известно, че времето и пространството са толкова тясно свързани помежду си, че представляват неделимо четиримерно пространство-време. Айнщайн постулира, че гравитацията трябва да бъде представена единствено по отношение на метричния тензор на четириизмерното пространство-време. За да изрази релативистичния закон на гравитацията, той изграждаше метричния тензор и тензора на кривината, образуван от него. След като той реши да се ограничи до тези градивни елементи, самата им слабост го доведе до по същество уникално тензорно уравнение за закона на гравитацията, при което гравитацията възниква не като сила, а като проява на кривината на пространството-времето.

Докато тензорите са били изучавани по-рано, успехът на общата теория на относителността на Айнщайн е породил сегашния широко разпространен интерес на математиците и физиците към тензорите и техните приложения.